Modelling by numbers
An introduction to procedural geometry
(This is the final part of a four part tutorial. If you haven’t already, you should check out Modelling by numbers: Part One A)

Part Two B: Making cylinders interesting
Unity assets – Unity package file containing scripts and scenes for this tutorial (all 4 parts).
Source files – Just the source files, for those that don’t have Unity.
Now we have some more interesting building blocks. Importantly, we now have the ability to make things with curves. This opens the door to so many shapes found in nature.
We’re going to have a look at two of them.
First, a mushroom


This is a more interesting object than a sphere or a cylinder, even though it’s basically an extension of those shapes.
We’ll start with the stem. There’s not much here we haven’t already learned to do – it’s just a cylinder with a bend:
Quaternion currentRotation = Quaternion.identity;
Vector3 currentOffset = Vector3.zero;
float stemBendRadians = m_StemBendAngle * Mathf.Deg2Rad;
float angleInc = stemBendRadians / m_StemHeightSegmentCount;
float stemBendRadius = m_StemHeight / stemBendRadians;
Vector3 startOffset = new Vector3(stemBendRadius, 0.0f, 0.0f);
for (int i = 0; i <= m_StemHeightSegmentCount; i++)
{
float heightNormalised = (float)i / m_StemHeightSegmentCount;
currentOffset = Vector3.zero;
currentOffset.x = Mathf.Cos(angleInc * i);
currentOffset.y = Mathf.Sin(angleInc * i);
float zAngleDegrees = angleInc * i * Mathf.Rad2Deg;
currentRotation = Quaternion.Euler(0.0f, 0.0f, zAngleDegrees);
currentOffset *= stemBendRadius;
currentOffset -= startOffset;
BuildRing(meshBuilder, m_StemRadialSegmentCount, currentOffset, m_StemRadius,
heightNormalised, i > 0, currentRotation);
}
Only one difference here. Instead of calculating the ring position and rotation as local variables inside the loop, we use variables outside of it. The result will be that these variables will end up containing the position and rotation of the final ring. Why do we want to do this? Well, this is where we are going to want to put the mushroom’s cap.

Now, the cap is a little more complicated. We could use half a sphere, but that wouldn’t look very natural, and would also leave us with less possibilities for variation. Instead of a circular cross-section, we’re going to use a Bézier curve.

A Bézier curve is curve defined by two or more control points. A cubic Bézier curve, the kind that we’ll be using, uses four points: the start and end, plus two additional controls.
Instead of defining four completely separate points and exposing those to the Unity editor, we can simplify things a little for our mushroom cap.
It’s helpful to think of the two middle control points as offsets from the end points, rather than separate points. Handles that define where the curve goes as it moves away from the end point.
The peak of the cap (the end point for the curve) will always be at the centre of the cap. To keep the mesh smooth at that point, the handle has to always be horizontal and pointing outwards. That handle, therefore, only needs a length to be defined. For the rim, we will use both a length and an angle.

Now, there are some things we need to calculate:
Vector3 capPeak = new Vector3(0.0f, m_CapThickness, 0.0f); Vector3 capRim = new Vector3(m_CapRadius, -m_CapHeight + m_CapThickness, 0.0f);
These are the positions at the ends of our curve. One at the very peak of the cap, and one at the edge of the rim. As with all our cross-section code so far, we’re working in the XY plane.
The positions are offset so that the base of the cap (ie. m_CapThickness below the peak) is at zero. This is so that when we offset by the position at the top of the stem, the cap will sit nicely on the stem.
Vector3 peakHandle = new Vector3(m_CapPeakHandleLength, 0.0f, 0.0f); float rimAngleRadians = m_CapRimHandleAngle * Mathf.Deg2Rad; Vector3 rimHandle = new Vector3(Mathf.Cos(rimAngleRadians), Mathf.Sin(rimAngleRadians), 0.0f); rimHandle *= m_CapRimHandleLength;
These are our Bézier handles, defined as offsets from their main points. The peak handle is always horizontal and so can just have its length plugged straight into the X value. The rim handle is defined by the angle from the X axis (note the use of trigonometric functions and thus the conversion to radians) and its length.
Now, the rest of our cap-building code goes into a separate function (so we can reuse it when it comes to building the gills). We pass in a position and rotation offset (the ones we ended up with after building the stem), as well as all four control points:
BuildCap(meshBuilder, currentOffset, currentRotation, capRim, capPeak, capRim + rimHandle, capPeak + peakHandle);
And the function looks like this:
void BuildCap(MeshBuilder meshBuilder, Vector3 offset, Quaternion rotation, Vector3 capRim,
Vector3 capPeak, Vector3 controlRim, Vector3 controlPeak)
{
int capHeightSegmentCount = m_CapRadialSegmentCount / 4;
for (int i = 0; i <= capHeightSegmentCount; i++)
{
float heightNormalised = (float)i / capHeightSegmentCount;
Vector3 bezier = Bezier(capRim, controlRim, controlPeak, capPeak, heightNormalised);
Vector3 centrePos = new Vector3(0.0f, bezier.y, 0.0f);
float radius = bezier.z;
Vector3 tangent = BezierTangent(capRim, controlRim, controlPeak,
capPeak, heightNormalised);
Vector2 slope = new Vector2(tangent.x, tangent.y);
BuildRing(meshBuilder, m_CapRadialSegmentCount, offset + rotation * centrePos,
radius, heightNormalised, i > 0, rotation, slope);
}
}
The code is similar to our sphere-building code. We are using our Bézier curve, rather than a vertical circle position, to offset height and radius values. The tangent is also generated from the curve.
Now for those Bézier functions:
Vector3 Bezier(Vector3 start, Vector3 controlMid1, Vector3 controlMid2, Vector3 end, float t)
{
float t2 = t * t;
float t3 = t2 * t;
float mt = 1 - t;
float mt2 = mt * mt;
float mt3 = mt2 * mt;
return start * mt3 + controlMid1 * mt2 * t * 3.0f + controlMid2 * mt * t2 * 3.0f + end * t3;
}
Vector3 BezierTangent(Vector3 start, Vector3 controlMid1, Vector3 controlMid2, Vector3 end, float t)
{
float t2 = t * t;
float mt = 1 - t;
float mt2 = mt * mt;
float mid = 2.0f * t * mt;
Vector3 tangent = start * -mt2 + controlMid1 * (mt2 - mid) +
controlMid2 * (-t2 + mid) + end * t2;
return tangent.normalized;
}
The maths involved here would take a tutorial of its own to explain. If you’re curious, check out this page for a good explanation (and cool interactive diagrams). Basically, what these functions do is interpolate along our Bézier curve by t and return either the position at that point on the curve, or the tangent.
Our mushroom so far:

Now we want gills on the underside of our cap. This will follow another curve, between the rim and a point below the peak.
We could add a second set of handle variables to define this curve, but that would make our shape more complicated than it needs to be. To keep things simple (and avoid having a bajillion variables to define the mushroom shape), most of the parameters of this inner curve can be calculated based on the outer curve. We’ll use the same peak handle, and rotate the rim handle 90 degrees.

To build our gills:
capPeak.y -= m_CapThickness; rimHandle = new Vector3(-rimHandle.y, rimHandle.x, 0.0f);
We’re offsetting the peak position by the cap thickness, and getting a rim handle 90 degrees away from the current one.
BuildCap(meshBuilder, currentOffset, currentRotation, capPeak, capRim, capPeak + peakHandle, capRim + rimHandle);
When we call BuildCap(), we reverse all the control points. You may remember this trick from when we built backfaces for our house roof. Instead of starting with the rim and interpolating through to the peak, we’re now going backwards, from peak to rim. This has the same effect as the roof plane trick, it makes our mesh face the opposite direction: in toward the stem rather than away from it.

Our mushroom is complete. Play with it a while to see the variety of shapes it can come up with. One cool thing it allows us to do is adjust the segment count values to high and low-poly versions of the same mesh:
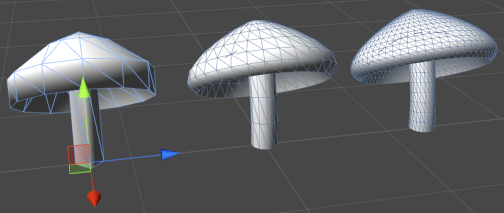
There we have it. Now, on to the final shape for this tutorial:
A flower


It looks like a really complex and difficult object, but the trick is to break it down into parts.
Before we get going making this mesh, I’ve got some Unity stuff to talk about. In particular, a problem that’s going to become more and more apparent the more complex your meshes become:
The price of complex objects, an inspector panel a million variables long
If you look back through all the shapes we’ve covered so far, you’ll see those Unity UI images getting taller and taller the more complicated our geometry gets, and the flower one is the tallest yet.
This isn’t just overwhelming for anyone using your script. It also means that you’re juggling more and more data in code. When building complex meshes, it’s worth looking into ways to address this.
First and foremost, think carefully about what really needs to be exposed. For the purposes of this tutorial, I’ve run with a kind of “expose everything” methodology, but often exposing too much will only lead to whoever uses your script to get confused and/or break it. Some things will do fine with a constant value seen only by the script. Others can be derived from data you already have.
To give an example, in our previous shape, the mushroom, we defined a variable to control the thickness of the cap. Unless your end-users are going to be spending a lot of time looking at the underside of that mesh, why not ditch that variable and always have the thickness equal to half the height of the cap?
Another way of dealing with all that data is to divide it into sections (or even into completely separate meshes). This is what we’re going to do with the flower script.
To do this in Unity, we define a class containing our variables and use [System.Serializable] to expose it to the editor:
[System.Serializable]
public class LeafPartData
{
public bool m_Build = true;
public float m_Width = 0.2f;
public float m_Length = 0.3f;
public float m_BendAngle = 90.0f;
public float m_StartAngle = 0.0f;
public float m_BendAngleVariation = 10.0f;
public float m_StartAngleVariation = 0.0f;
public int m_Count = 6;
public int m_WidthSegmentCount = 8;
public int m_LengthSegmentCount = 8;
public bool m_BuildBackfaces = true;
}
public LeafPartData m_SepalData;
public LeafPartData m_PetalData;
This gives us two sections in the Unity inspector called Sepal Data and Petal Data, nicely labeled, sectioned off and, even more nicely, collapsable.
Plus we have the usual advantages that come with dividing your code up into objects: we can reuse them, and we can pass them around easily.
Now, shall we build something?
Let’s get back to our flower. First things first, let’s give it a stem:
void BuildStem(MeshBuilder meshBuilder, out Vector3 currentOffset, out Quaternion currentRotation,
CylinderData partData)
{
currentOffset = Vector3.zero;
currentRotation = Quaternion.identity;
if (!partData.m_Build)
return;
float stemBendRadians = partData.m_BendAngle * Mathf.Deg2Rad;
float angleInc = stemBendRadians / partData.m_HeightSegmentCount;
float stemBendRadius = partData.m_Height / stemBendRadians;
Vector3 startOffset = new Vector3(stemBendRadius, 0.0f, 0.0f);
for (int i = 0; i <= partData.m_HeightSegmentCount; i++)
{
float heightNormalised = (float)i / partData.m_HeightSegmentCount;
currentOffset = Vector3.zero;
currentOffset.x = Mathf.Cos(angleInc * i);
currentOffset.y = Mathf.Sin(angleInc * i);
float zAngleDegrees = angleInc * i * Mathf.Rad2Deg;
Quaternion rotation = Quaternion.Euler(0.0f, 0.0f, zAngleDegrees);
currentOffset *= stemBendRadius;
currentOffset -= startOffset;
BuildRing(meshBuilder, partData.m_RadialSegmentCount, currentOffset,
partData.m_Radius, heightNormalised, i > 0, currentRotation);
}
}
It’s packaged up into its own function this time, but this code should be getting familiar by now. Our stem is a bent cylinder. As with our mushroom, we keep the position and rotation in external variables, so that we know where to put the flowerhead. All the variables have been bundled up into a CylinderData class, instead of passing each one in one by one.
Something else that data class contains (as will all the data classes for this flower) is an m_Build boolean value. This provides the ability to turn parts of the flower on and off. Allowing simpler meshes for scenes that require them, or for hiding the bits we’re not working on to better see the bits we are.

On to our flowerhead. We’ll do the middle part next, the part in the centre of the petals. In nature, this is not a single component, it is the business section of a flower and it can get quite complicated. We’re going to simplify, however. So much that all we’re going to do is build a sphere. What we will add is the ability to flatten the sphere a little, using a vertical scale value.
void BuildHead(MeshBuilder meshBuilder, Vector3 offset, Quaternion rotation, SphereData partData)
{
if (!partData.m_Build)
return;
float angleInc = Mathf.PI / partData.m_HeightSegmentCount;
float verticalRadius = partData.m_Radius * partData.m_VerticalScale;
for (int i = 0; i <= partData.m_HeightSegmentCount; i++)
{
Vector3 centrePos = Vector3.zero;
centrePos.y = -Mathf.Cos(angleInc * i);
float radius = Mathf.Sin(angleInc * i);
Vector2 slope = new Vector3(-centrePos.y / partData.m_VerticalScale, radius);
slope.Normalize();
centrePos.y = centrePos.y * verticalRadius + verticalRadius;
radius *= partData.m_Radius;
Vector3 finalRingCentre = rotation * centrePos + offset;
float v = (float)i / partData.m_HeightSegmentCount;
BuildRing(meshBuilder, partData.m_RadialSegmentCount, finalRingCentre, radius,
v, i > 0, rotation, slope);
}
}
First, note that we have again written our function to bail out if this part is turned off with m_Build.
A slope value is calculated from the circular position (rotated 90 degrees to get a tangent and adjusted by the vertical scale).
The Y position is multiplied by the vertical radius instead of the normal radius. The Y position also has the vertical radius added to it. This offsets the sphere so that its base is on zero, rather than its centre. This sits it on top of the stem, rather than having the stem end in the middle of it.
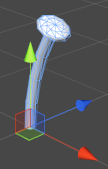
OK, now for a slightly more complicated bit. We’re going to build petals for our flower. The first thing we need to know about these is that they’re not cylinders. To make them, we need to go all the way back to the code we used to build our ground plane. To make our petals (and sepals, and any other leafy part of the flower), we need a grid.
void BuildLeafPart(MeshBuilder meshBuilder, Vector3 offset, Quaternion rotation,
LeafPartData partData)
{
for (int i = 0; i <= partData.m_LengthSegmentCount; i++)
{
float z = (partData.m_Length / partData.m_LengthSegmentCount) * i;
float v = (1.0f / partData.m_LengthSegmentCount) * i;
float xOffset = -partData.m_Width * 0.5f;
Vector3 normal = rotation * Vector3.up;
for (int j = 0; j <= partData.m_WidthSegmentCount; j++)
{
float x = (partData.m_Width / partData.m_WidthSegmentCount) * j;
float u = (1.0f / partData.m_WidthSegmentCount) * j;
Vector3 position = offset + rotation * new Vector3(x + xOffset, 0.0f, z);
Vector2 uv = new Vector2(u, v);
bool buildTriangles = i > 0 && j > 0;
BuildQuadForGrid(meshBuilder, position, uv, buildTriangles,
partData.m_WidthSegmentCount + 1, normal);
}
}
}
Our grid code from way back, modified. As before, we have a pair of loops incrementing an XZ offset, and calling BuildQuadForGrid(). We’ve added position and rotation offsets that need to be applied to the vertex offset and the normal, plus there’s an X offset of half the width of the grid. What this does is offset our grid so that zero is at the bottom middle, instead of the bottom corner. The leafy parts of our flower can now join to the flower by the middle.
When we call this function, we need to use a rotation that moves the petals around in a circle:
void BuildLeafRing(MeshBuilder meshBuilder, Vector3 offset, Quaternion rotation,
float radius, LeafPartData partData)
{
if (!partData.m_Build)
return;
for (int i = 0; i < partData.m_Count; i++)
{
float yAngle = 360.0f * i / partData.m_Count;
Quaternion radialRotation = rotation * Quaternion.Euler(0.0f, yAngle, 0.0f);
Vector3 position = offset + radialRotation * Vector3.forward * radius;
BuildLeafPart(meshBuilder, position, radialRotation, partData);
}
}
This is the code that builds our whole ring of petals. For our rotation, we simply use a Euler rotation in the Y axis that moves from 0 to 360 degrees.
We are also pushing the position away from the middle of the circle by a radius value. This is so that the petals will originate around the outside of the stem, rather than from the middle of it.
The result looks something like this:

Next, we’re going to want to add a curve. To do this, we use the same method we use to bend a cylinder, except that we do it to a plane, instead.
void BuildLeafPart(MeshBuilder meshBuilder, Vector3 offset, Quaternion rotation,
LeafPartData partData)
{
float bendAngleRadians = partData.m_BendAngle * Mathf.Deg2Rad;
float angleInc = bendAngleRadians / partData.m_LengthSegmentCount;
float bendRadius = partData.m_Length / bendAngleRadians;
Vector3 startOffset = new Vector3(0.0f, bendRadius, 0.0f);
for (int i = 0; i <= partData.m_LengthSegmentCount; i++)
{
float v = (1.0f / partData.m_LengthSegmentCount) * i;
float xOffset = -partData.m_Width * 0.5f;
Vector3 centrePos = Vector3.zero;
centrePos.y = Mathf.Cos(angleInc * i);
centrePos.z = Mathf.Sin(angleInc * i);
float bendAngleDegrees = (angleInc * i) * Mathf.Rad2Deg;
Quaternion bendRotation = Quaternion.Euler(bendAngleDegrees, 0.0f, 0.0f);
centrePos *= bendRadius;
centrePos -= startOffset;
Vector3 normal = rotation * (bendRotation * Vector3.up);
for (int j = 0; j <= partData.m_WidthSegmentCount; j++)
{
float x = (partData.m_Width / partData.m_WidthSegmentCount) * j;
float u = (1.0f / partData.m_WidthSegmentCount) * j;
Vector3 position = offset + rotation *
new Vector3(x + xOffset, centrePos.y, centrePos.z);
Vector2 uv = new Vector2(u, v);
bool buildTriangles = i > 0 && j > 0;
BuildQuadForGrid(meshBuilder, position, uv, buildTriangles,
partData.m_WidthSegmentCount + 1, normal);
}
}
}
There, now we’ve added the familiar bend code. We calculate a circle in the ZY plane and use this to rotate each row in the grid, just like we rotate each ring when bending a cylinder.

Notice that our petals are rectangular. Often, we will want to leave it this way and define the petal shape using a texture with an alpha channel. But since we’re concentrating on meshes rather than textures here, there’s a simple way to make it more interesting:
void BuildLeafPart(MeshBuilder meshBuilder, Vector3 offset, Quaternion rotation,
LeafPartData partData)
{
float bendAngleRadians = partData.m_BendAngle * Mathf.Deg2Rad;
float angleInc = bendAngleRadians / partData.m_LengthSegmentCount;
float bendRadius = partData.m_Length / bendAngleRadians;
Vector3 startOffset = new Vector3(0.0f, bendRadius, 0.0f);
for (int i = 0; i <= partData.m_LengthSegmentCount; i++)
{
float v = (1.0f / partData.m_LengthSegmentCount) * i;
float localWidth = partData.m_Width * Mathf.Sin(v * Mathf.PI);
float xOffset = -localWidth * 0.5f;
Vector3 centrePos = Vector3.zero;
centrePos.y = Mathf.Cos(angleInc * i);
centrePos.z = Mathf.Sin(angleInc * i);
float bendAngleDegrees = (angleInc * i) * Mathf.Rad2Deg;
Quaternion bendRotation = Quaternion.Euler(bendAngleDegrees, 0.0f, 0.0f);
centrePos *= bendRadius;
centrePos -= startOffset;
Vector3 normal = rotation * (bendRotation * Vector3.up);
for (int j = 0; j <= partData.m_WidthSegmentCount; j++)
{
float x = (localWidth / partData.m_WidthSegmentCount) * j;
float u = (1.0f / partData.m_WidthSegmentCount) * j;
float bendAngleDegrees = (angleInc * i) * Mathf.Rad2Deg;
Quaternion bendRotation = Quaternion.Euler(bendAngleDegrees, 0.0f, 0.0f);
Vector2 uv = new Vector2(u, v);
bool buildTriangles = i > 0 && j > 0;
BuildQuadForGrid(meshBuilder, position, uv, buildTriangles,
partData.m_WidthSegmentCount + 1, normal);
}
}
}
All we are doing is adding a multiplier to the width of each row. In this case, the multiplier is generated with a sine wave. This shrinks the width in toward each end, giving us a nicer shape:

Looking decent, but it’s too flat. The petals curl, but still radiate out from the center on a completely flat plane. This will limit the amount of variation we can make with this script. We want the ability to rotate the petals inwards/outwards from the base. We’ll do this by using a starting angle and having the bend begin with this, instead of an angle of zero.
void BuildLeafPart(MeshBuilder meshBuilder, Vector3 offset, Quaternion rotation,
LeafPartData partData)
{
float bendAngleRadians = partData.m_BendAngle * Mathf.Deg2Rad;
float angleInc = bendAngleRadians / partData.m_LengthSegmentCount;
float bendRadius = partData.m_Length / bendAngleRadians;
float startAngleRadians = partData.m_StartAngle * Mathf.Deg2Rad;
Vector3 startOffset = Vector3.zero;
startOffset.y = Mathf.Cos(startAngleRadians) * bendRadius;
startOffset.z = Mathf.Sin(startAngleRadians) * bendRadius;
for (int i = 0; i <= partData.m_LengthSegmentCount; i++)
{
float v = (1.0f / partData.m_LengthSegmentCount) * i;
float localWidth = partData.m_Width * Mathf.Sin(v * Mathf.PI);
float xOffset = -localWidth * 0.5f;
Vector3 centrePos = Vector3.zero;
centrePos.y = Mathf.Cos(angleInc * i + startAngleRadians);
centrePos.z = Mathf.Sin(angleInc * i + startAngleRadians);
float bendAngleDegrees = (angleInc * i + startAngleRadians) * Mathf.Rad2Deg;
Quaternion bendRotation = Quaternion.Euler(bendAngleDegrees, 0.0f, 0.0f);
centrePos *= bendRadius;
centrePos -= startOffset;
Vector3 normal = rotation * (bendRotation * Vector3.forward);
for (int j = 0; j <= partData.m_WidthSegmentCount; j++)
{
float x = (localWidth / partData.m_WidthSegmentCount) * j;
float u = (1.0f / partData.m_WidthSegmentCount) * j;
Vector3 position = offset + rotation *
new Vector3(x + xOffset, centrePos.y, centrePos.z);
Vector2 uv = new Vector2(u, v);
bool buildTriangles = i > 0 && j > 0;
BuildQuadForGrid(meshBuilder, position, uv, buildTriangles,
partData.m_WidthSegmentCount + 1, normal);
}
}
}
Before the loop, we use the start angle to calculate an offset to be applied to all our position offsets. This forces the base of the sepal to stay in the same place.
Inside the loop, we simply add our start angle to our incremented angle before doing any calculations with it.

Now, let’s address a problem in our current mesh. If we were to look at it from below, our petals would be invisible. We’re going to build a back side for each petal. We can reuse our BuildLeafPart() function for this, but it needs some minor adjustments:
void BuildLeafPart(MeshBuilder meshBuilder, Vector3 offset, Quaternion rotation,
LeafPartData partData, bool isBackFace)
{
float bendAngleRadians = partData.m_BendAngle * Mathf.Deg2Rad;
float angleInc = bendAngleRadians / partData.m_LengthSegmentCount;
float bendRadius = partData.m_Length / bendAngleRadians;
float startAngleRadians = partData.m_StartAngle * Mathf.Deg2Rad;
Vector3 startOffset = Vector3.zero;
startOffset.y = Mathf.Cos(startAngleRadians) * bendRadius;
startOffset.z = Mathf.Sin(startAngleRadians) * bendRadius;
float backFaceMultiplier = isBackFace ? -1.0f : 1.0f;
for (int i = 0; i <= partData.m_LengthSegmentCount; i++)
{
float v = (1.0f / partData.m_LengthSegmentCount) * i;
float localWidth = partData.m_Width * Mathf.Sin(v * Mathf.PI) * backFaceMultiplier;
float xOffset = -localWidth * 0.5f;
Vector3 centrePos = Vector3.zero;
centrePos.y = Mathf.Cos(angleInc * + startAngleRadiansi);
centrePos.z = Mathf.Sin(angleInc * i + startAngleRadians);
float bendAngleDegrees = (angleInc * i + startAngleRadians) * Mathf.Rad2Deg;
Quaternion bendRotation = Quaternion.Euler(bendAngleDegrees, 0.0f, 0.0f);
centrePos *= bendRadius;
centrePos -= startOffset;
Vector3 normal = rotation * (bendRotation * Vector3.up) * backFaceMultiplier;
for (int j = 0; j <= partData.m_WidthSegmentCount; j++)
{
float x = (localWidth / partData.m_WidthSegmentCount) * j;
float u = (1.0f / partData.m_WidthSegmentCount) * j;
Vector3 position = offset + rotation *
new Vector3(x + xOffset, centrePos.y, centrePos.z);
Vector2 uv = new Vector2(u, v);
bool buildTriangles = i > 0 && j > 0;
BuildQuadForGrid(meshBuilder, position, uv, buildTriangles,
partData.m_WidthSegmentCount + 1, normal);
}
}
if (!isBackFace && partData.m_BuildBackfaces)
BuildLeafPart(meshBuilder, offset, rotation, partData, true);
}
We pass in a boolean value to let the function know if it’s currently building back faces, and it uses this to do a couple of things. Firstly, it reverses the width value and the normal. Reversing the width causes each row to be built backwards, flipping the direction of the resulting quads and thus the triangle winding order. Reversing the normal means that lighting will also work correctly on the reverse side.
Lastly, the function checks if it currently building back faces, and if not, calls itself in order to do so. Note that the part data contains a variable to disable this. This is useful if we know that the flowerhead is never going to be seen from behind.
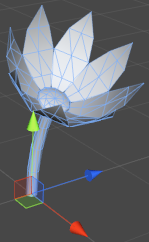
Next, we’re going to add a bit more visual interest to our flower by adding some randomness to the bend and start angles. This way each petal will bend and pivot with a slightly different angle, resulting in a more natural appearance.
Remember that BuildLeafRing() effectively gets called twice per petal. This means we can’t do anything random inside that function or the front and back sides won’t line up. For this to work, the angles will need to be calculated outside BuildLeafPart() and passed in as arguments, rather than having BuildLeafPart() use the values from the part data.
void BuildLeafRing(MeshBuilder meshBuilder, Vector3 offset, Quaternion rotation,
float radius, LeafPartData partData)
{
if (!partData.m_Build)
return;
for (int i = 0; i < partData.m_Count; i++)
{
float yAngle = 360.0f * i / partData.m_Count;
Quaternion radialRotation = rotation * Quaternion.Euler(0.0f, yAngle, 0.0f);
Vector3 position = offset + radialRotation * Vector3.forward * radius;
float bendAngleRandom = Random.Range(-partData.m_BendAngleVariation,
partData.m_BendAngleVariation);
float bendAngle = partData.m_BendAngle + bendAngleRandom;
float startAngleRandom = Random.Range(-partData.m_StartAngleVariation,
partData.m_StartAngleVariation);
float startAngle = partData.m_StartAngle + startAngleRandom;
BuildLeafPart(meshBuilder, position, radialRotation, partData, false,
bendAngle, startAngle);
}
}
Now each petal has a little bit of uniqueness to it:

Now on to the next part of the flower: the sepals (the leafy parts underneath the flowerhead). Actually, these are exactly the same as our petals, with different values defined in the part data. To build them, we simply call BuildLeafRing() again.
BuildLeafRing(meshBuilder, currentPosition, currentRotation, m_StemData.m_Radius, m_SepalData);

And that’s our flower. To recap, the top-level code to build it looks like this:
Vector3 currentPosition; Quaternion currentRotation; //main stem: BuildStem(meshBuilder, out currentPosition, out currentRotation, m_StemData); BuildHead(meshBuilder, currentPosition, currentRotation, m_HeadData); //sepals: BuildLeafRing(meshBuilder, currentPosition, currentRotation, m_StemData.m_Radius, m_SepalData); //petals: BuildLeafRing(meshBuilder, currentPosition, currentRotation, m_StemData.m_Radius, m_PetalData);

This script is expandable, for those feeling up to it. If we wanted, we could easily add extra rows of petals here. Simply define more LeafPartData objects for them and keep calling BuildLeafRing(). A similar method could be used to add leaves to the stem.
And that’s this tutorial complete. Well done. Now, go and play with what you’ve learned, and build something awesome.


Awesome tutorials. This code based modelling is really interesting to me, and opens up cool ideas as far as generating random worlds and adaptive changing worlds. Is there a point in complexity where it becomes too inefficient to model through coding or are the limitations mostly artistic?
Hi Jayelinda, we have a common interest in procedural geometry! I like what you are doing and how you are presenting it. In case it is not on your radar yet, I’d recommend checking a 3d graphic language from the 80ies called GDL, and in particular the gdl cookbook pdf that describes that very simple yet powerful 3d procedural/parametric language. I am amazed that somebody coming from a graphic background also finds that path interesting. With a good formalization, it can be so much faster indeed to learn and create objects than a conventional 3d editor. I am currently exploring the possibility of something similar that would eventually reside completely on the GPU. In your list of advantages, I would add automatic lod generation. My background is game programming (mostly C/C++ although I also played a bit with Unity) but an issue with electromagnetic frequencies forced me a few years ago to take a long break away from the screens. I am currently catching up in particular with GPU programming, but it should not take too long. I will use this in a crowd sourcing project I am piloting from home where kids will be able to reconstruct in 3D their neighborhood and visualize improvements with more vegetation for example. If you have an interest in any of this or for your own project, please let me know.
Cordially.
Michel Royer
Amazing tutorial with some great ideas. Although I don’t think I have the time to build everything out just triangles/quads and will likely just use it for the ground, it was great to learn how to generate more complex mesh’s.
Thanks for making it!
Hey Jayelinda! You are truly awesome 🙂 Thanks for sharing all this and presenting the infos so nicely!
Cheerio,
Peter
I love your clear, concise, and down to earth instruction style. I wish more teachers took a page from your book.
BTW, I think there is a typo in your code example just below, “Let’s get back to our flower. First things first, let’s give it a stem:”, where you build the stem:
Quaternion rotation = Quaternion.Euler(0.0f, 0.0f, zAngleDegrees);
I believe the variable should be named currentRotation?